Example
Asian Indices
The trading of options on Asian indices like KOSPI, NKY, HSI, etc has been a very competitive game for a while. In the last few years trading of Indian indices has exploded, becoming by some metrics the most traded options in the world. (If you want to talk about fitting NIFTY and BANKNIFTY, please contact us). Market data acquisition, implying forwards, accurate and robust vol curve/surface fitting, temporal filtering (aka “smoothing” of microstructure noise, outlier detection, etc), and many other issues have become quite non-trivial problems to solve.
Our clients have found our robust and super-fast fitting infrastructure to be extremely helpful in taking one hard, tedious and time-consuming problem off their plate, so that they can concentrate on where they really have an edge in the trading of these products. Our clients have also found that our sensible and intuitive vol curves are very easy to extrapolate into the dark books that exist for maturities beyond 1 or 2 years to expiry.
Before we turn to some examples, a word of caution about the raw data, especially in the wings. We’re using as inputs to our fitter purely snapshots of bid and ask options prices. The data in the wings often suffer from “tick size quantization issues” that arise when there is e.g. a bunch of puts = 0.02 x 0.03 for a set of strikes, followed by a bunch of 0.01 x 0.02 for a couple of smaller strikes. Clearly the best estimate of the raw option microprices here is not just the mid. Our clients, at least the low-latency ones, use more sophisticated microprices as input to the fitter, taking into account sizes and higher levels of the order book, often with a little bit of smoothing over time (our library provides tools to deal with all this). This resolves many of the tick size quantization issues on the level of the input microprices. Our fitter is therefore handicapped when receiving the naive mids as inputs, but arguably does an excellent job even in the wings given this handicap, as we will see.
Now, some examples… we concentrate on the hardest to fit terms in the front months:
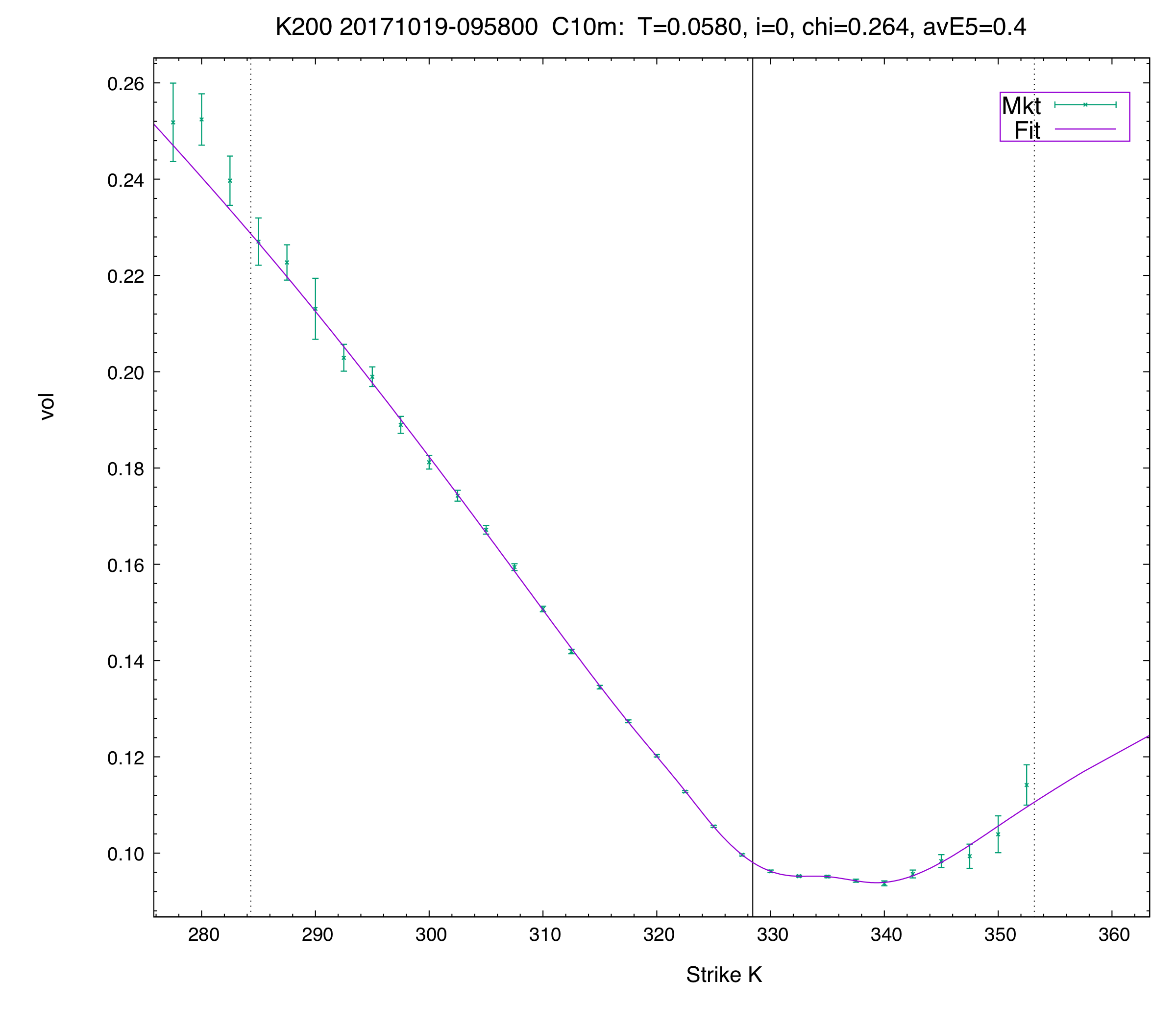
C10 vol fit of the first term for the KOSPI. The wiggle on the call side is real (it lasts hours, if not the whole day) and has to be fitted for an accurate valuation. Here both the call and put wings provide illustrations of the tick size quantization issues mentioned above. For example, the last two calls shown in the call wing are both C = 0.01 x 0.02 in the data we’re using. The calls at the two strikes just before are 0.02 x 0.03 and 0.05 x 0.06, respectively. Arguably the fitted vol curve does a good job given these inputs (and better microprices tend to confirm this: in all cases where we were able to compare fitted vols and theos from naive and more fancy microprices there is virtually no difference in the final results).
One could actually use our 12- or 14-parameter curves in this case. Our fitter can fit these high parameter curves perfectly robustly and the fit in the put wing becomes a bit better below a normalized strike of -6 or so. Whether this is the right thing to do is debatable given the above facts, but, in any case, the fits from the different curves are virtually identical -- and tradeable -- for the 20-odd strikes from NS = -5 to +2.
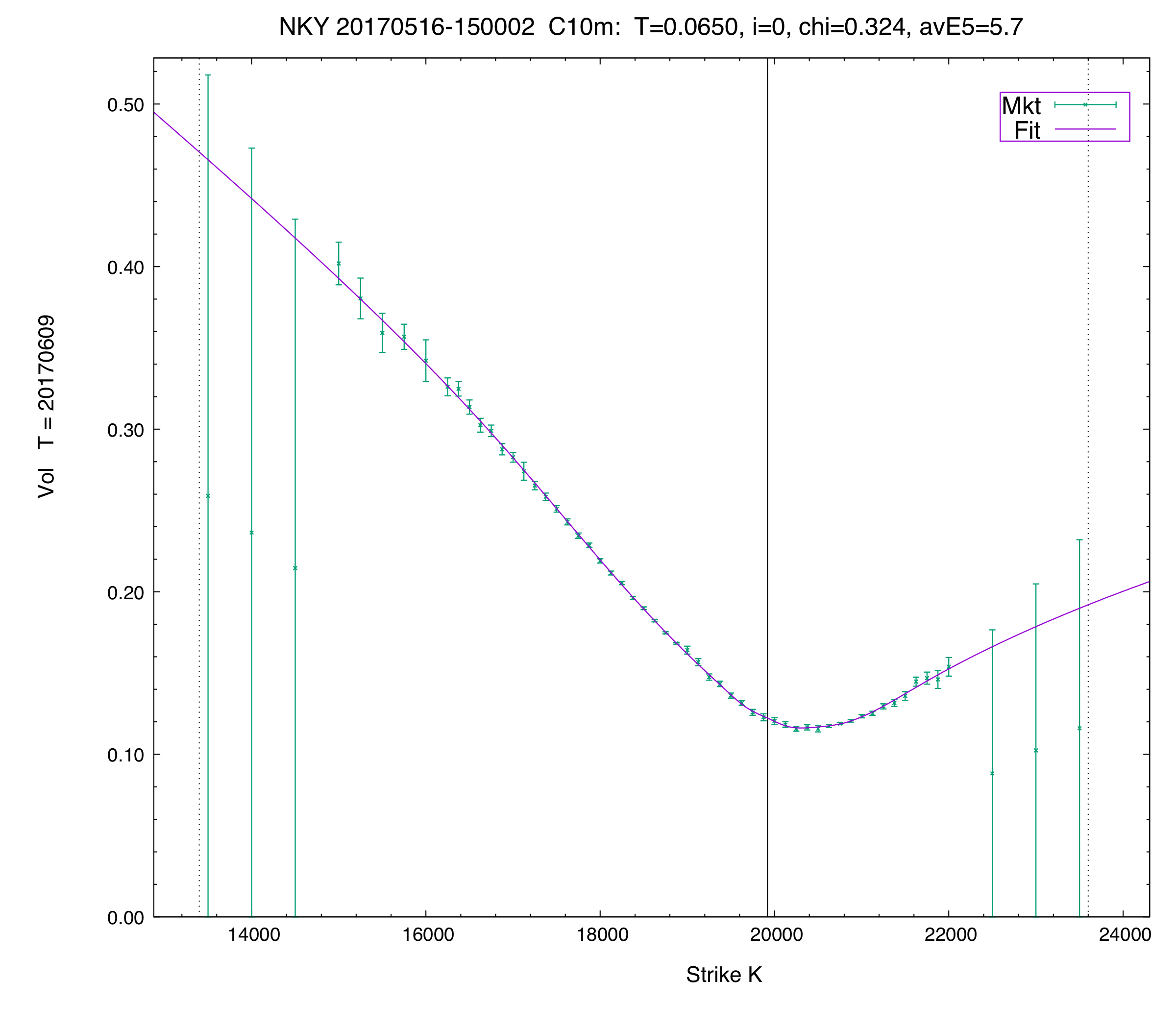
C10 vol fit of the first term in the Nikkei.
Note that the zero-bid options in the wings drag down the mid-market prices & mid-market implied volatilities, but Vola's fitter (robustly) does not drag its implied volatility curve substantially lower in either wing.
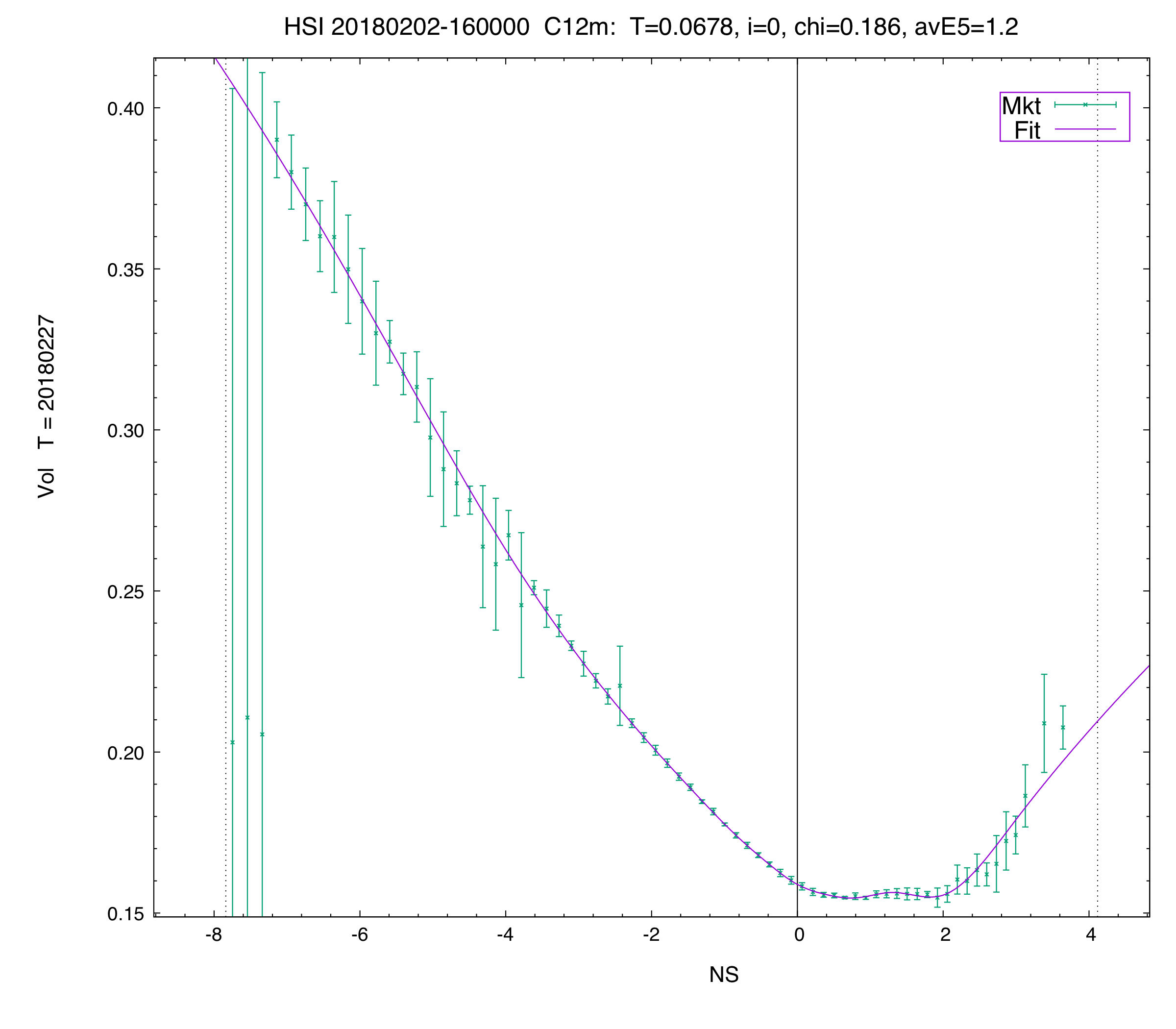
C12 vol fit of the first term in the HSI.
The HSI is an interesting example. The data available to us here are of rather questionable quality, with a lot of fake non-zero bids (that are really zero-bids), and other quotes, especially for ITMs, that are clearly quite off. Our filtering and fitting analytics can nevertheless imply accurate forwards, vols, and arbitrage-free parametric vol curves/surfaces in a very robust fashion. In this sense, this is a really good example for the robustness of our analytics.
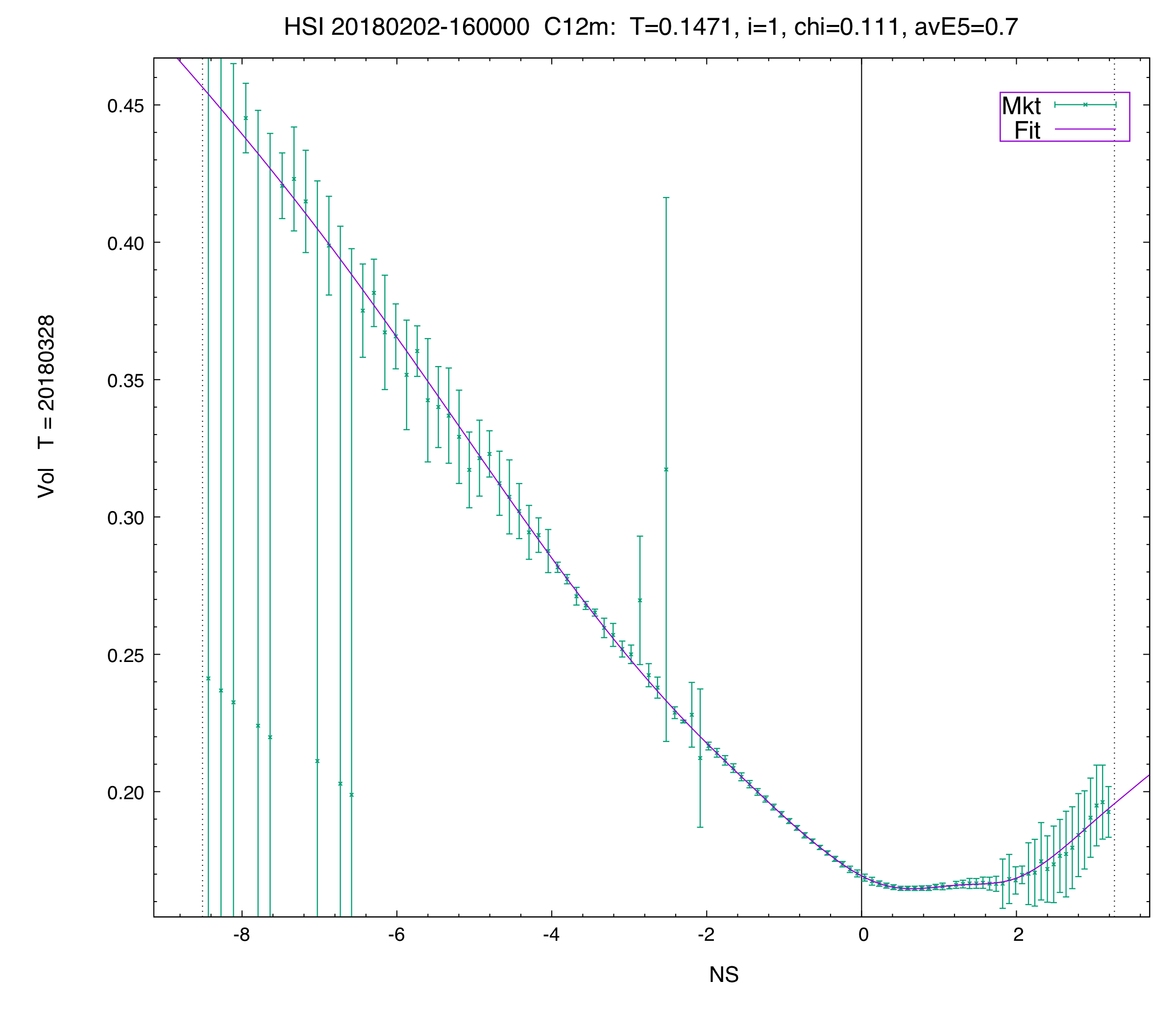
C12 vol fit of the second term in the HSI.
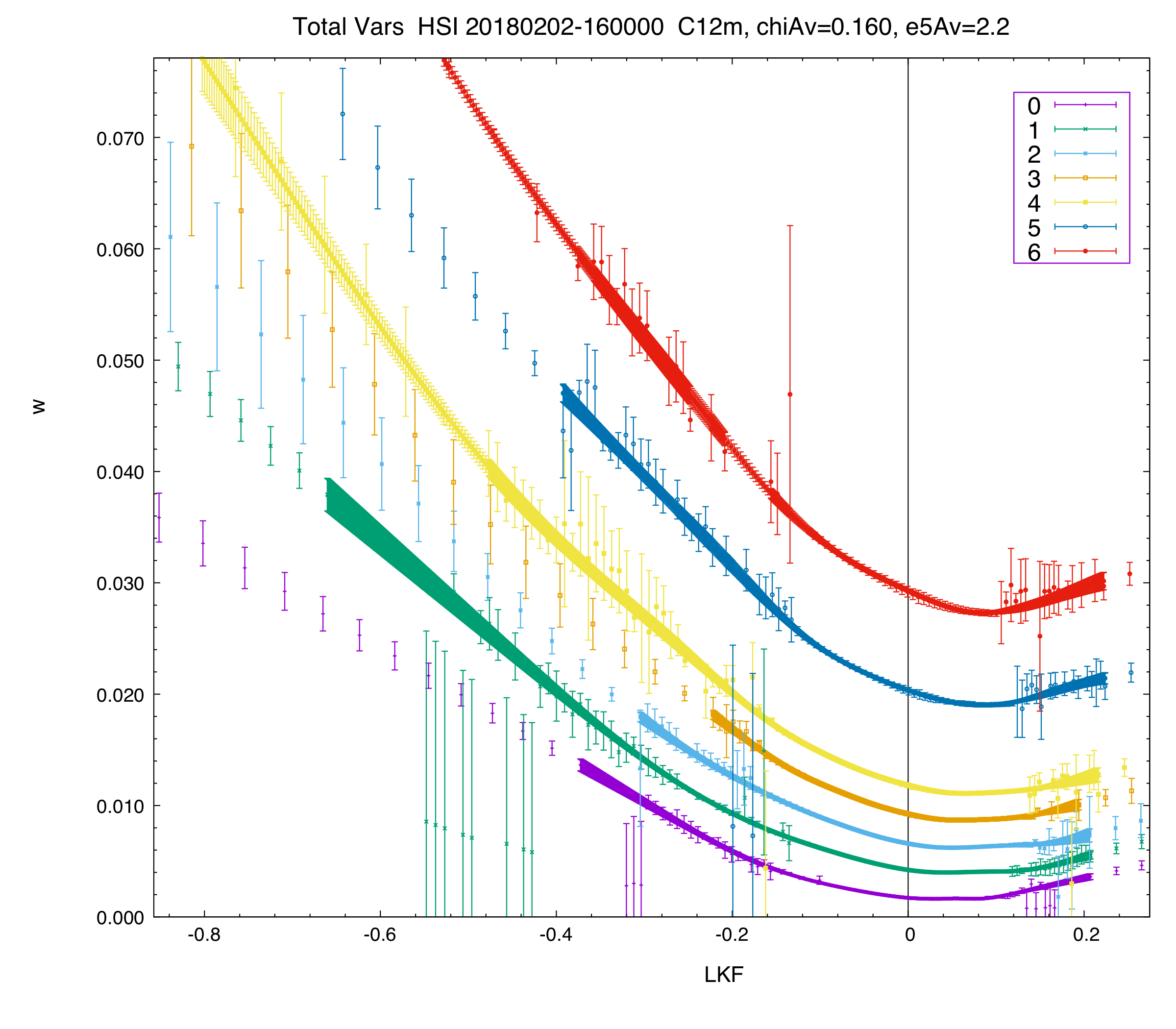
Total variance plot of the first seven HSI expiries.
Note, these 'total variance' curves, as plotted in this manner, are in sequential order by time-to-expiry and are non-intersecting — a necessary and sufficient condition for lack of calendar arbitrage.